Traces of Surface X2 + Y2 âë†â€™ Z2 = 1: Determine the Equation for the Family of Traces in X = N.

Quick Overview

• To observe the equation of a line you need a point and a gradient.
• The slope of the tangent line is the value of the derivative at the indicate of tangency.
• The normal line is a line that is perpendicular to the tangent line and passes through the point of tangency.

Examples

Example 1

Suppose $$f(x) = 10^3$$. Find the equation of the tangent line at the point where $$x = 2$$.

Pace 1

Notice the point of tangency.

Since $$10=2$$, we evaluate $$f(two)$$.

$$ f(ii) = ii^three = eight $$

The point is $$(two,8)$$.

Step 2

Notice the value of the derivative at $$x = two$$.

$$ f'(x) = 3x^2\longrightarrow f'(2) = 3(ii^2) = 12 $$

The the slope of the tangent line is $$thou = 12$$.

Step 3

Find the signal-slope grade of the line with slope $$k = 12$$ through the bespeak $$(2,8)$$.

$$ \begin{align*} y - y_1 & = m(ten-x_1)\\[6pt] y - 8 & = 12(x-ii) \cease{align*} $$

Answer

$$y - 8 = 12(10-two)$$

For reference, here is the graph of the function and the tangent line nosotros just found.

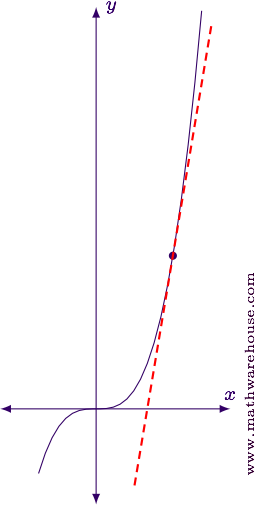
Instance 2

Suppose $$f(x) = ten^2 - ten$$. Find the equation of the tangent line with slope $$m = -3$$.

Step 1

Notice the derivative.

$$ f'(x) = 2x -ane $$

Step 2

Find the $$ten$$-value where $$f'(x)$$ equals the slope.

$$ \brainstorm{align*} f'(ten) & = 2x -i\\[6pt] -3 & = 2x -1\\[6pt] -2 & = 2x\\[6pt] 10 & = -1 \finish{marshal*} $$

Step three

Observe the point on the role where $$x = -1$$.

$$ f(-1) = (-1)^two - (-one) = 1 + 1 = ii $$

The point is $$(-1, 2)$$.

Pace 4

Detect the equation of the line through the signal $$(-1,2)$$ with slope $$m=-three$$.

$$ \begin{align*} y -y_1 & = m(ten-x_1)\\[6pt] y - 2 & = -3(x - (-1))\\[6pt] y - 2 & = -three(x+1) \end{align*} $$

Answer

$$ y - 2 = -iii(ten+1) $$

For reference, here's the graph of the function and the tangent line we but found.

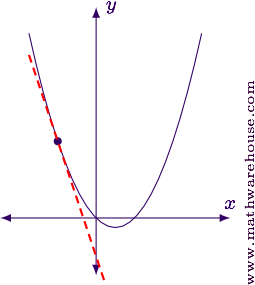
Tangent Lines to Implicit Curves

The procedure doesn't change when working with implicitly defined curves.

Instance 3

Suppose $$x^2 + y^2 = 16$$. Detect the equation of the tangent line at $$x = two$$ for $$y>0$$.

Stride 1

Discover the $$y$$-value of the betoken of tangency.

$$ \begin{align*} \blue{x^2} + y^2 & = 16\\[6pt] \blue{two^2} + y^2 & = xvi\\[6pt] \blue{four} + y^2 & = xvi\\[6pt] y^2 & = 12\\[6pt] y & = \pm\sqrt{12}\\[6pt] y & = \pm\sqrt{four\cdot 3}\\[6pt] y & = \pm2\sqrt three \end{align*} $$

Since the problem states we are interested in $$y>0$$, we utilise $$y = 2\sqrt 3$$.

The point of tangency is $$(2, 2\sqrt three)$$.

Stride 2

Notice the equation for $$\frac{dy}{dx}$$.

Since the equation is implicitly defined, we use implicit differentiation.

$$ \begin{align*} 2x + 2y\,\frac{dy}{dx} & = 0\\[6pt] 2y\,\frac{dy}{dx} & = -2x\\[6pt] \frac{dy}{dx} & = -\frac{2x}{2y}\\[6pt] \frac{dy}{dx} & = -\frac x y \terminate{marshal*} $$

Step 3

Find the gradient of the tangent line at the point of tangency.

At the point $$(2,2\sqrt iii)$$, the gradient of the tangent line is

$$ \begin{align*} \frac{dy}{dx}\bigg|_{(\blue{two},\red{2\sqrt three})} & = -\frac {\blue 2} {\red{2\sqrt 3}}\\[6pt] & = -\frac 1 {\sqrt 3}\\[6pt] & = -\frac 1 {\sqrt 3}\cdot \blueish{\frac{\sqrt 3}{\sqrt three}}\\[6pt] & = -\frac{\sqrt 3} 3 \end{align*} $$

The slope of the tangent line is $$m = -\frac{\sqrt 3} iii$$.

Step four

Notice the equation of the tangent line through $$(2,two\sqrt three)$$ with a slope of $$chiliad=-\frac{\sqrt three} 3$$.

At the point $$(2,2\sqrt iii)$$, the slope of the tangent line is

$$ \begin{align*} y - y_1 & = m(x-x_1)\\[6pt] y - 2\sqrt three & = -\frac{\sqrt 3} 3(x-2) \end{align*} $$

Answer

The equation of the tangent line is $$y - 2\sqrt 3 = -\frac{\sqrt 3} three(10-2)$$

For reference, the graph of the curve and the tangent line we found is shown below.

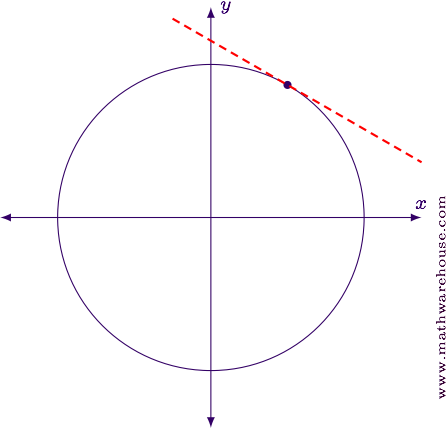
Normal Lines

Suppose nosotros have a a tangent line to a role. The function and the tangent line intersect at the point of tangency. The line through that same indicate that is perpendicular to the tangent line is called a normal line.

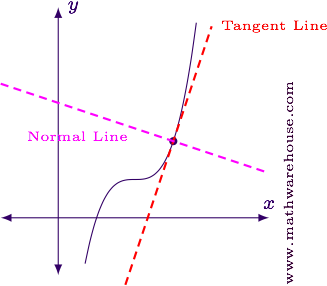
Recall that when 2 lines are perpendicular, their slopes are negative reciprocals. Since the slope of the tangent line is $$m = f'(x)$$, the slope of the normal line is $$m = -\frac i {f'(x)}$$.

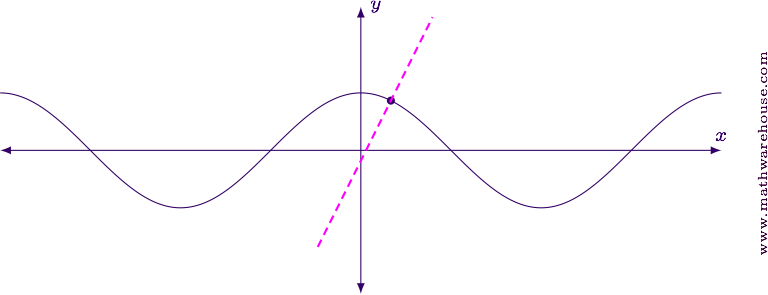
Example 4

Suppose $$f(x) = \cos x$$. Find the equation of the line that is normal to the office at $$x = \frac \pi 6$$.

Stride 1

Find the point on the part.

$$ f\left(\frac \pi vi\right) = \cos \frac \pi 6 = \frac{\sqrt 3} ii $$

The betoken is $$\left(\frac \pi 6, \frac{\sqrt 3} 2\right)$$.

Step ii

Detect the value of the derivative at $$x = \frac \pi half dozen$$.

$$ f'(10) = -\sin x\longrightarrow f'\left(\frac \pi 6\right) = -\sin\frac\pi six = -\frac 1 2 $$

The slope of the tangent line is $$yard = -\frac 1 2$$. Since we are looking for the line that is perpendicular to the tangent line, nosotros desire to apply $$k = ii$$.

Pace 3

Detect the equation of the line through the indicate $$\left(\frac \pi 6, \frac{\sqrt 3} 2\right)$$ with a gradient of $$m =2$$.

$$ \begin{marshal*} y -y_1 & = yard(ten-x_1)\\[6pt] y - \frac{\sqrt iii} two & = 2\left(10 - \frac \pi half dozen\right) \end{align*} $$

Reply

The line normal to the function at $$x = \frac \pi vi$$ is $$y - \frac{\sqrt iii} 2 = ii\left(x - \frac \pi 6\right)$$.

For reference, here is the graph of the function and the normal line nosotros found.

Continue to Practice Issues

Error : Please Click on "Non a robot", then try downloading again.

ramirezviscruend.blogspot.com

Source: https://www.mathwarehouse.com/calculus/derivatives/how-to-find-equations-of-tangent-lines.php

Share this post